Under the action of self-gravity, the initial conditions and hydrodynamic evolution of protostar formation inside molecular cloud cores are not yet fully explored; these are key problems to be solved in frontier astrophysics which also become a very active research field involving mutual interactions between observations and theoretical development. Nowadays by dust extinction effects observed in molecular cloud cores, it is possible to infer the mass density profiles in several prestellar molecular cloud cores. As a rough preliminary first approximation, thus derived mass density profile in a molecular cloud core may be grossly described by the spherically symmetric, static, isothermal Lane-Emden equation (i.e. Bonnor-Ebert sphere). Nevertheless, more and more astronomical observations and theoretical investigations in recent years indicate that molecular clouds on larger scales and molecular cloud cores on smaller scales are not really static and are most likely in a stage of hydrodynamic evolution under self-gravity; depending on specific situations, such dynamic evolution may be either fast or slow. With this perspective, we have substantially generalized and extended the static isothermal Lane-Emden equation to include the main physical feature of radial hydrodynamic bulk flow in order to establish a theoretical evolution model involving general polytropic self-similar hydrodynamics. Meanwhile, we proved the homology theorem for this new dynamic Lane-Emden equation and used its solution to better fit the classical molecular cloud core Barnard 68 (B68) in several major aspects of observationally acquired data. This class of physical models can be equally invoked to describe gravitational collapse processes of forming gaseous planets and brown dwarfs in relatively isolated Mini Gas Globules (MGGs) and so forth.
Generally speaking, protostar formation is initiated by gravitational collapses of molecular cloud cores. In a global description framework of spherical symmetry and based on a self-similar hydrodynamic transformation and general polytropic equation of state, we have comprehensively analyzed in depth the ideal hydrodynamic equation involving the self-gravity,and eventually derived the dynamic Lane-Emden equation involving the radial inertial force. In the vicinity of the cloud core center, we established the recursion relation for the coefficients of a series expansion and thus obtained the asymptotic solution for this series expansion; we also obtained singular solutions diverging towards the cloud center. By satisfying the central physical boundary conditions, we derived several analytical solutions and obtained many numerical solutions by extensive exploration. As a concrete example among other astrophysical applications, we modelled the physical properties of prestellar cloud core B68 based on the study of the dynamic Lane-Emden equation. In fact, our general polytropic dynamically collapsing solution fits B68 better in several observational aspects than the static isothermal Bonner-Ebert sphere does (Alves, Lada & Lada, 2001, Nature, 459, 159) and infers the pertinent dynamic timescale to be about several hundred thousand years. Our comparative analysis of theoretical models clearly indicates that a mere model fit of the radial distribution of mass density profile within a cloud core does not necessarily determine all major physical properties of the core system. In particular, we would emphasize that the theoretical model of static isothermal Bonner-Ebert sphere as fitted by Alves et al. (2001) for B68 data is known to be unstable; as a result, such a cloud core cannot remain static and should evolve in time in a dynamic manner.
Entirely parallel to this type of theoretical model analysis for general polytropic hydrodynamics, we can study the dynamic evolution of an infinitely long uniform cylinder with axisymmetry. Certain results become different because of distinct geometries for sphere and cylinder. Long mass filaments under self-gravity appear on various temporal and spatial scales in various contexts of astrophysics and cosmology. Perturbations along such a long uniform cylinder can induce Jeans instability so that clumps or segments or clumps embedded in segments along the long cylinder. This mechanism can explain and predict the appearance of sequences and chains of astrophysical objects such as chains of gaseous planets or brown dwarfs, stars, galaxies, black holes, clusters of galaxies and so forth.
The research results of our theoretical analysis for dynamic evolution model and consistent data fits for B68 in several aspects have been officially published in the well-known international journal -- Monthly Notices of the Royal Astronomical Society (Li, Lou, Esimbek, MNRAS,2018,437,2441). The authors are DaLei Li (associate researcher) and Jarken Esimbek (researcher) of XingJiang Astronomical Observatory and Professor Yu-Qing Lou (corresponding author) of Tsinghua University. This research project has been supported by grants from National Natural Science Foundation of China, the Programme of the Light in China’s Western Region, the China Ministry of Science and Technology, Tsinghua University Initiative Scientific Research Programme, special PhD training programmes of the Ministry of Education. Website Link:https://doi.org/10.1093/mnras/stx1925
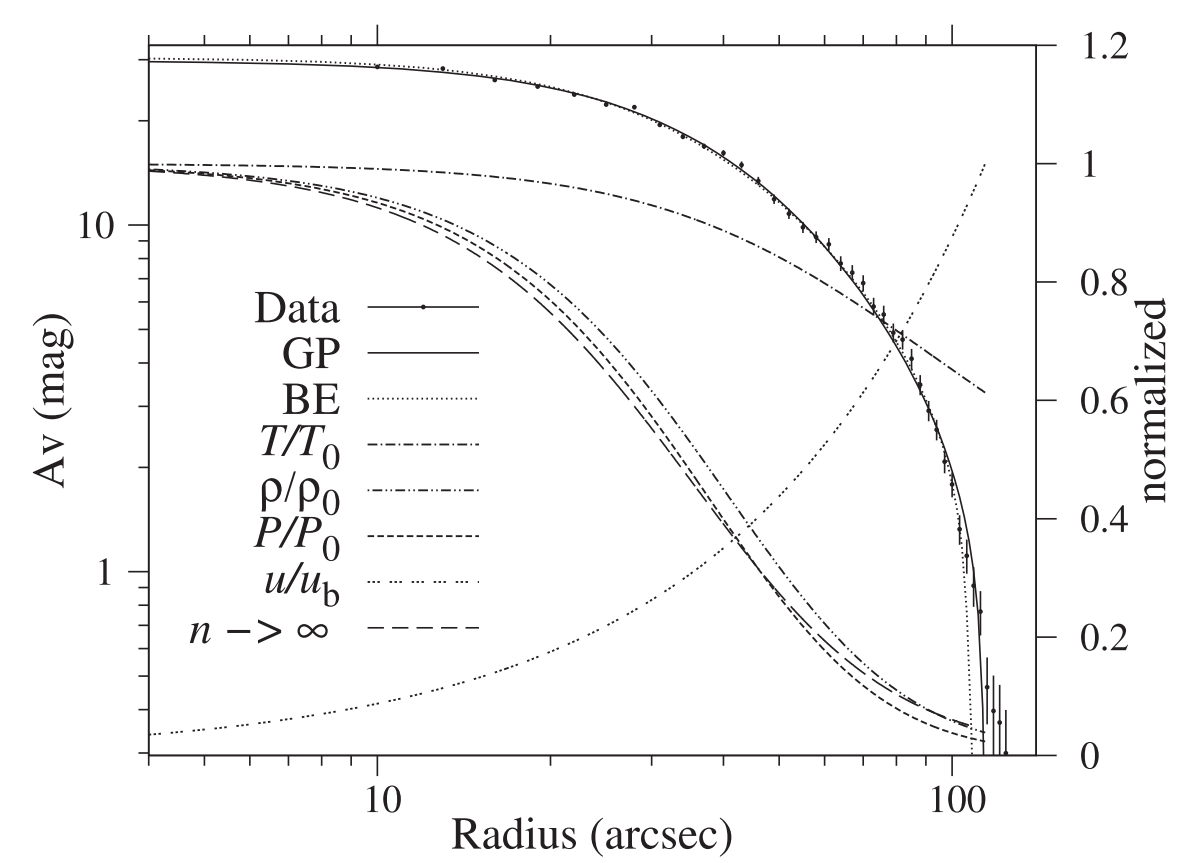
Figure 1: Comparison of general polytropic dynamic evolution model versus static isothermal Bonnor-Ebert sphere model for the molecular cloud core B68 in terms of radial profile for the mass density distribution as well as other pertinent results. Small solid dots with vertical bars with relatively larger spacings are dust extinction data with error bars. The dotted curve represents the static isothermal Bonnor-Ebert sphere model (Alves et al. 2001); the solid curve represents the solution of our general polytropic solution of the dynamic Lane-Emden equation (Li, Lou, Esimbek 2018) with two fitting parameters n=6.65 and c=0.00867; other relevant curves are: the dash-dotted curve (T/T0) is the normalized temperature profile with the central temperature T0 being 10 K; the dash-dot-dotted curve (rho/rho 0) is the normalized mass density profile with the central mass density rho 0 being 1.4 X 10^{-18} gram per cubic centimeter; the dashed curve(P/P0)is the normalized molecular gas pressure profile with the central pressure being P0=5.02 X 10^{-11} Pa; the triple dotted curve (u/u b) is the normalized inward radial flow speed with the radial speed at the outer boundary u b being 0.11 km per second. The long dashed curve (n approaching infinity) is the normalized mass density profile derived from the Lane-Emden equation, i.e. the mass density solution from the static isothermal Bonnor-Ebert sphere model.

Figure 2: Professor Yu-Qing Lou (left), Researcher Jarken Esimbek (right), DaLei Li (background)